Comprendiendo Matemática para Cuarto Año: mayo 2016

FUNCIÓN

MATEMÁTICA

Trabajo práctico N°1

Fecha de presentación:

Lunes 16 - 05 -2016 (4° año "A" )

Lunes 16 - 05 -2016 (4° año "E" )

Jueves 19- 05 - 2016 (4°año "B" )

1. Dibuja un sistema de coordenadas

cartesianas;

a)Señala los puntos A=(3,5); B=(-2,1);

C=(-3,-2); D=(2,2)

b) Une los puntos señalados.

c) ¿Qué figura es el cuadrilátero ABCD?

d) Decide si cada uno de los puntos que

se dan están o no en el cuadriláteros ABCD:

P=(1/2,2); Q=(1,5); R=(-1,0); S=(-2,-1).

2. a) Representa en un sistema de

coordenadas cartesianas:

i)Tres puntos que tengan abscisa -1.

ii)Todos los puntos que tienen abscisa-1.

iii)Dos puntos que tengan ordenada 4.

iV)Todos los puntos que tienen ordenada 4.

b)De las coordenadas del único punto que

cumple las dos condiciones a la vez.

Representa en el plano.

3.a)Decide si P=(3,0);

Q=(0,1); T=(3/2,5);

W=(6,1); X=(-2,-3)

pertenecen al semiplano sombreado.

b)Encuentra tres valores de

x para que B=(x,5) pertenezca

al semiplano sombreado.

c)Si A=(x,5), ¿cómo debe ser la abscisa x

para que A esté en el semiplano sombreado?

4. En un sistema de coordenadas

cartesianas:

a) Sombréa la zona que corresponda a los puntos del

plano que tienen ordenada y<5.

b) Indica cuáles de los siguientes puntos pertenecen

a la zona sombreada:

A=(0,0) B=(-3,-4) C=(5,-5) D=(1,7)

5.Indica en qué cuadrante está cada uno de los

siguientes puntos:

A=(-1,2) B=(2,3) C=(2.-1) D=(-2,-5) E=(-2,2)

F=(1,-1) G=(1/2,2/5) H=(2,-2/3) I=(2,5) J=(10,-3)

---------------------------------------
-------------------------
--------

Consejos para el trimestral

1°) Para el trimestral debe repasar todo lo visto en clase

desde FUNCIONES.

2°) Resuelve los siguientes ejercicios:

a) Tres de estos cinco puntos pertenecen al gráfico de la

función de R en R: y = 3x + 2. Indique ¿cuáles son?:

A=( 1;5) B=( 2;6) C=(-2; -4) D=(1/3 ;3) E=( 0 ; 3)

b) Escriba tres pares ordenados que pertenezcan y dos pares

que no pertenezcan al gráfico de la función lineal:

y = (-1/5)x + 3

c) Los puntos A, B, C, D y E pertenecen al gráfico de la

función lineal y = 2x - 5. Complete los valores que faltan.

A=(0;.....) B=(1/4; ....) C=(.....; 0) D=(.....; 2/5) E=(...;...)

d)Grafique las funciones ( distinto color ):

y=3

y = (2/3)x - 4

y= - 5x + 2

e) Proponga tres funciones constantes no nulas y

grafíca en un par de ejes cartesianos.

f) Represente en un mismo sistema de coordenadas, las

siguientes funciones lineales (distinto color):

y=3x + 1 y= -3x + 4 y= 2x - 1

y = 3x - 4 y= 2x + 3

Responde: En el ejercicio anterior ( f ):

f.1-¿Se trata de funciones crecientes o decrecientes?

Nombre o clasifique

f.2-¿cuáles son crecientes y cuáles decrecientes?

f.3-¿Cómo te has dado cuenta?

Compara sus ecuaciones .

f.4- ¿Cómo son las pendientes de

dos rectas paralelas?

f.5- Escribe las fórmulas de las rectas paralelas.

g) Representa en un mismo sistema de coordenadas,

empleando la misma escala en los dos ejes. ( distinto color )

y= -5x + 2 y = (1/5)x - 3 y= -5x

y = (3/4)x - 1 y=(-4/3)x + 5

Mira los gráficos que hiciste y responde:

g.1-Nombra ¿cuáles de estas rectas son perpendiculares?

g.2- ¿Qué número se obtiene al multiplicar las pendientes

de dos rectas perpendiculares?

h)Escribe la ecuación de una recta que sea

perpendicularidad y otra que sea paralela a

y = 2x + 5

CONSULTA EL LUNES Y MARTES

Ejercicio extra:

Mira la figura y observa q tienes que tener en cuenta a la

hora de ubicar un punto en un sistema de ejes

cartesianos.

Video:

https://www.youtube.com/watch?v=jlKv4Vugy8c

Escribe ¿qué coordenadas tienen los puntos indicados

en la figura?

Si tu respuesta fue Q=(4,-5) R=(-5,2) P=( 6,3) , has entendido. Realiza las actividades 4 y 5 nuevamente. Suerte!!!!!!

----------------------------------

Recordemos:

Gráficos de funciones

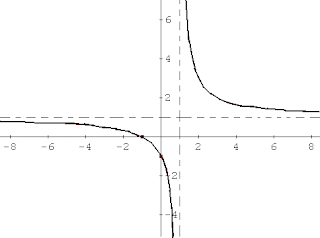
Los que ven a continuación son gráficos de funciones.

Puedes decir¿por qué?

Busca otros ejemplos, dónde las variables se relacionen y

determinen una función útil para analizar.

Recordemos la definición de función:

Una función asigna un único valor de la variable y a cada valor de la variable x.

x es una variable independiente.

y, que es función de x, es una variable dependiente.

Se escribe y=f(x)

El término función fue usado por primera vez
en 1637 por el matemático francés René Descartes.

------------------------------------------------------------

6. Explica porqué las gráficas que se muestran en las figuras a) y b) no son gráficas de una función.
a)

Funciones lineales

https://prezi.com/kut5ag38f600/copy-of-funcion-lineal/

Entre los tipos de funciones posibles hay uno especialmente importante, cuya gráfica es una recta o parte de ella. Los fenómenos que describen se caracterizan porque la variación de la variable dependiente es proporcional a la variación de la variable independiente.

Una función lineal se expresa de la forma:

y = mx+b ó f(x)= mx+b

con m y b números reales.

Tiene las siguientes características:

es una función cuya representación gráica es una recta.
m (coeficiente de x) es la pendiente, expresa la variación de la variable y cuando x aumenta una unidad.
b es la ordenada al origen, la recta corta al eje y en el punto(0,b)

Ejemplo 1

Vimos en clase que con dos valores en la tabla es suficiente, pero un tercer valor
nos asegura que nuestros cálculos son correctos.

Mira el siguiente video : ubicar puntos y gráfico de una función lineal

https://www.youtube.com/watch?v=KH9xznJynWg

IMPORTANTE: recuerda que debes traer

la neetbook para trabajar en la próxima clase

y se le solicita a los alumnos que busquen

y lean en su domicilio el software Geogebra

y el tutorial:

http://www.geogebra.org/help/geogebraquickstart_es.pdf,

que podrán utilizar.
El programa, se lo puede descargar del sitio oficial de

GeoGebra:
http://www.geogebra.org/cms/es/download/,

gratuitamente, por si no lo tienen instalado y acceder

también a muchos tutoriales y aplicaciones.

Les comento que es importante dedicarle unos minutos

al software para explorar las herramientas con las que

cuenta y conocer las diferentes vistas.

Deben concurrir con su neetbook, con baterías
con carga suficiente como para poder trabajar
sin inconvenientes.

^{8.Considere la función y = -2x + 3, ¿Qué}

valor toma f(x) cuando x = -1 ?

^{a) 1 b) 0 c)-1 d) 5 e) 2}

^{9. Sea f(x) = 2x + 4, ¿Qué valor toma la}

variable dependiente cuando la variable

independiente toma valor 1?

^{a) 6 b) 3/2 c)-2/3 d) -7 e) -3/2}

10. Dada la siguiente ecuación: y = (1/2)x - (1/2). ¿Qué valor toma la función cuando la abscisa se hace igual a 2?

a) -5 b) 0 c) 5 d) -2 e)1/2

11. Dada la función y = -x + 2, ¿Para qué valor de la variable independiente la función toma el valor 1?

a) -1 b) 0 c)3 d)1 e) -2

12.Sea la función f(x) = 4x - 8, ¿Para qué valor de la abscisa f(x) vale 4?

a) 2 b) 3 c) 8 d) -3 e) -8

13.Dada la función y = 4x + 4, ¿Para qué valor de "x" la variable "y" toma valor de cero?

a) 2 b)1 c) 0 d) -1 e) -2

14. Complete el siguiente cuadro:

función	¿ Qué valor toma la variable dependiente cdo. la abscisa es igual a 3?	¿Para qué valor de la variable independiente la ordenada toma valor 2?	¿Pasa por el par (1,-5)?
Y = 2x + 5
Y= -x + 3

15. Dada la función y = 2x + 2, su gráfica corta al eje de las abscisas en:
a) 2 b) 0 c) -2 d) 1 e) -1

16. Dada la siguiente ecuación: y = 2x + 5, el par ordenado que corresponde a la intersección de la gráfica con las ordenadas es:
a) (2,5) b) (5,0) c) (0, -5) d) ( 0,0) e) (0,5)

17. Dada la siguiente función: y = 4x - 2, el par ordenado que corresponde a la intersección de la gráfica con las abscisas es :
a) (1/2,0) b) (4;0) c) (0,4) d) ( -2,0) e) (0,1/2)

18. Sea f(x) = 4x - 1. La ordenada al origen vale:
a) 4 b) -4 c) -1 d) 1/4 e) 1

19. Considere la función y= -2x + 3. Su gráfica corta al eje de las ordenadas en:
a) 3/2 b) 0 c) -2 d) 2 e) 3

20. Dada la función y = 5x - 2, en la representación gráfica la recta corta en :
a) 2 de la ordenada
b) -2 de la ordenada

c)2/5 de la abscisa
d) 2 de la abscisa
e) b y c son correctas

21. Dada la función y=(1/7)x, su gráfica corta al eje de las abscisas en:
a) 1/7 b) 7 c) 0 d) -7 e) 3

22. Considere la siguiente función: y= 5x - 10
a) ¿Qué valor toma la variable dependiente cuando la abscisa vale 3?

b)¿Para que valor de la función la variable independiente se hace igual a -1?

c )¿Cuánto vale la ordenada si la abscisa se hace igual a la unidad?

d)¿Qué valor toma la ordenada cuando la abscisa se anula?

e)¿Cuánto vale la variable independiente cuando la variable dependiente vale -30?

f)¿Qué valor toma la abscisa cuando la función toma valor 20?

g)¿Cuánto vale la variable independiente cuando la ordenada vale - infinito?

h)Determine el punto de corte con el eje de ordenadas ("y") y expréselo en forma de par ordenado.

i)Determine el punto de corte con el eje de abscisa ("x") y expréselo como par ordenado.

j)¿Pasa la función por el punto (4,12)?

k) ¿Pasa la función por el par (-3,-25)?

Rtas.